
harsha kokel
Advice based relational learning
As part of an independent study with Prof. Sriraam Natarajan, I read advice-based methods for data in relational first-order logic. Here are my notes on it.
Artificial Intelligence (AI) is rapidly becoming one of the most popular tool for solving various problems of humankind. Ranging from trivial day-to-day activity of switching on/off lights, to severe life-changing decision of detecting tumors in scans, all the problems have been tackled with this tool and hence it is no longer acceptable to have a black-box algorithm making calls. AI Community has realized this and hence has put lot of significance on Explainable AI (XAI) in recent years. AI research has taken a shift from Human vs Robot to Human-Allied AI or Human-in-the-loop AI. However, this is not an unexplored territory. Advice-based or Knowledge-based methods have been around since the conception of AI.
Advice based method
Lot of work has been done to incorporate knowledge in propositional domain and was surveyed by me as part of CS 7301 Recent Advances in Computing - Survey of Adv Research in CS in Fall of 2018. I summarize it here and then review the work done in relational domain.
Usually advice-based methods encode human knowledge or domain information in various forms, a small list with examples is provided below.
- A set of if-then rules is represented as propositional horn clauses
Advice: if $B_1, B_2, …, B_n$ then $A$
Horn clause: $A \leftarrow B_1, B_2, …, B_n$ - Qualitative influence between variables is rendered as Qualitative Probabilistic Network (QPN) (Wellman 1990)
Advice: “price of apple rises with an increase in demand”
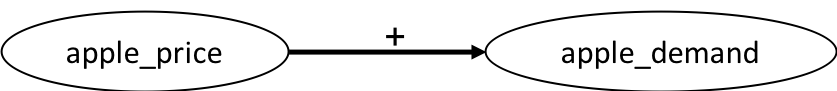
-
Uncertainty between variables is formulated by conditional probability tables
Advice: “When it is cloudy, it mostly rains”
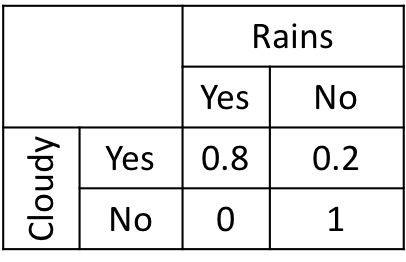
-
Preference statements under a ceteris paribus (all else being equal) is interpreted as CP-Net (Boutilier et al., 2004)
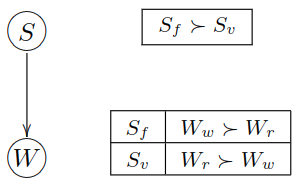
Advice: Fish soup ($S_f$) is strictly preferred over Vegetable soup ($S_v$), and preference between red ($W_r$) and white ($W_w$) wine is conditioned on the soup. Red wine is preferred if served with a vegetable soup, and white wine is preferred if served with a fish soup
Once advice is encoded, it is used while learning the model in one of the following ways:
-
Theory Refinement Advice is used as initial model with approximate domain knowledge and training examples are then used to refine this model.
-
Objective Refinement Advice is used to constrain or modify the objective function and then training samples are used to learn a model that maximizes this objective.
-
Observation Refinement Advice is used to refine, clean or augment part ( or all ) of the observed training samples and then this is used to learn the model.
Relational and SRL methods
Most of the real-world data is complex, attempts are made to represent them using object (as variables) and relations (as predicates) using first-order logic programs called Inductive Logic Programming (ILP). Add uncertainty to such complex data and they become convoluted. Multiple formalisms have been proposed for such probabilistic-logic representations using statistical techniques, now popular known as field of Statistical Relational Learning (SRL) (Getoor 2007). With power of complex representation, these model lose out on other tasks. Specifically, inference and learning (which involves inference) in SRL is NP-hard or harder. For that reason, learning SRL models have been a topic of interest among researchers for a long time and it called for advice-based learning.
Advice-based relational methods
First-order logic unlike propositional logic or flat feature vectors have two important linguistic features, viz. variables and quantifiers. These features augment capability of providing a general high-level advice for example we can say “Do not change lanes if there is no vehicle in front of you” which can be easily written as
\[ \begin{aligned} lane(x, l)\ \wedge\ &\neg\ \exists\ y,\ (\ lane(y, l)\ \wedge\ ahead(y, x)\ )\ \\ &\implies \ \neg\ changelane(x) \end{aligned} \]
One straight forward way of advice-based relational model is to hand-code the predicates or clauses without need of any data. Pazzani and Kibler (1992) proposed one of the first successful algorithms for advice-based inductive learning called First Order Combined Learner (FOCL). FOCL is an extension of FOIL (Quinlan, 1990). FOCL uses both inductive as well as explanation-based component (a set of horn clauses provided by human expert) to propose an extension to a learned concept at every step. FOCL has been shown to generalize more accurately than the purely inductive FOIL algorithm. Bergadano and Giordana (1988) had also proposed ML-SMART, to integrate explanation-based learning (EBL) and inductive techniques to construct operational concept definitions using three components: theory guided component, arbitrary component and a drop component. ML-SMART is able to handle both overly-general and overly-specific theories. The goal is to find rules that cover the positive examples of the concept and exclude the negatives. GRENDEL (Cohen, 1992) is another FOIL based system that uses advice in the form of an antecedent description grammar (ADG) to explicitly represent the inductive hypothesis space. Mooney and Zelle (1994) reviews advice-based methods developed for ILP which integrate ILP with EBL.
SRL models have probabilities (parameters) associated with the clauses (structure). Most raw form of advice in SRL can be direct probability values. But, there has been lot of work to incorporate richer form of advice. I briefly describe a few studies:
– Yang et al. 2014 proposed a cost-sensitive soft margin approach to learn from imbalanced domain. It builds up on the Relational Functional Gradient Boosting (RFGB) (Natarajan et al., 2012) approach of learning an SRL model by including a cost-augmented scoring function equation below that treats positive and negative examples differently in the objective function.
$$ c\left(\hat{y_{i}}, y\right)=\alpha I\left(\hat{y_{i}}=1 \wedge y=0\right)+\beta I\left(\hat{y_{i}}=0 \wedge y=1\right) $$
where $\hat{y_{i}}$ is the true label of $i^{th}$ instance and $y$ is the predicted label. $I(\hat{y_{i}} = 1 \wedge y = 0)$ is 1 for false negatives and $I(\hat{y_{i}} = 0 \wedge y = 1)$ is 1 for false positives. Hence, $c(\hat{y_{i}}, y) = \alpha$ when a positive example is misclassified, while $c(\hat{y_{i}},y) = \beta$ when a negative example is misclassified.
$$ \log J =\sum_{i} \psi\left(y_{i} ; \mathbf{X}{i}\right)- \log \sum{y_{i}^{\prime}} \exp \left\{ \psi\left(y_{i}^{\prime} ; \mathbf{X}{i}\right)+c\left(\hat{y}{i}, y_{i}^{\prime}\right) \right\} $$
Taking derivation of this modified objective function gives a nice form of gradient
$$\Delta=I\left(\hat{y}_{i}=1\right)-\lambda P\left(y_i=1 ; \mathbf{x}_i\right)$$
where $\lambda=\frac{e^{c\left(\hat{y}_{i}, y=1\right)}}{\sum_{y^{\prime}}\left[P\left(y^{\prime} ; \mathbf{X}_{i}\right) e^{c\left(\hat{y}_{i}, y^{\prime}\right)}\right]}$
Relational regression trees are then learnt using this soft-gradient.
– Odom et al. 2015 uses preference advice encoded in Horn clause form as a relational advice constraint and use it as cost function while learning the model.
A relational advice constraint (RAC), F is defined using a Horn clause $\wedge_i f_i(x_i) \implies label(x_e)$, where $\wedge_i f_i(x_i)$ specifies the conjunction of conditions under which the advice applies on the example arguments $x_e$. Each \textit{relational advice rules} (RAR) is defined using the triple $\langle F, l+, l- \rangle$ where $F$ is the RAC clause specifying the subset of examples, $l+$ is the preferred label and $l-$ is the avoided label. And, each relational advice set (RAS), $R$ is specified as a set of RAR. Cost function is defined as:
$$ c\left(x_{i}, \psi\right)=-\lambda \times \psi\left(x_{i}\right) \times\left[n_{t}\left(x_{i}\right)-n_{f}\left(x_{i}\right)\right] $$
where, $n_t$ indicates the number of advice rules that prefer the example to be true, $n_f$ the number of rules that prefer it to be false, $\lambda$ is scaling factor of the cost function and $\psi(x_i)$ is the current value of the $\psi$ function for the $x$.
The modified log-likelihood function is:
$$ MLL(\mathbf{x}, \mathbf{y})=\sum_{x_{i} \in \mathbf{x}} \log \frac{\exp \left(\psi\left(x_{i} ; y_{i}\right)\right)}{\sum_{y^{\prime}} \exp \left(\psi\left(x_{i} ; y^{\prime}\right)+c\left(y_{i}, y^{\prime}, \psi\right)\right)} $$
Scaled gradient of this is
$$ \eta \Delta\left(x_{i}\right) =\alpha \cdot \left[ I\left(y_{i}=1\right)-P\left(y_{i}=1 ; \psi\right) \right] + (1 - \alpha) \cdot\left[n_t\left(x_i\right)-n_f\left(x_i\right)\right] $$
So, when the example label is preferred target in more advice models than the avoided target, $n_t(x_i)-n_f(x_i)$ is set to be positive. This will result in pushing the gradient of these examples in the positive direction. And, $\alpha$ is the linear trade-off between data and advice.
This approach was successfully adapted in relation extraction and healthcare problems (Odom et al., 2015a; Soni et al., 2016; Natarajan et al., 2017).
– Later, Odom and Natarajan (2018) extended that constraint-based framework from Odom et al. (2015b) by redefining $l+$ and $l-$ in relational advice rules (RAR) triple $\langle F, l+, l- \rangle$ to weighted label. $\beta_t$ weight for preferred label and $\beta_f$ for the avoided label and modifying the cost function.
$$ c_{LP}\left(x_{i}, \psi\right)=-\lambda \times \psi\left(x_{i}\right) \times\left[\beta_{t} \times n_{t}\left(x_{i}\right)-\beta_{f} \times n_{f}\left(x_{i}\right)\right] $$
This enables them to include following types of advice:
- Preferential advice: This advice is handled similar to the previous paper, except now magnitude of each constraint is determined by the weights $\beta s$
- Cost-based advice: The soft margin approach in Yang wt al. 2014 is contained in the framework by controlling $\beta s$. Specifically, $\beta_t$ handles the sensitivity to false positives and $\beta_f$ for false negatives.
- Qualitative constraints: In relational domain advice on qualitative constraints can be viewed as providing multiple pieces of advice over a given feature. As the number of objects satisfying this constraint increases more advice will apply. $n_t$ (or $n_f$ ) to scale based on that feature.
- Privileged information: This is the features that are available during training but not during testing. To handle this, they define a cost function that reduces the KL divergence between $P(y|x)$ and $P(y|x^{RP})$ where $x^{RP}$ is the set of all the features including privilege features.
$$ c_{R P}\left(x_{i}, \psi\right) = -\lambda \times K L\left(P_{D}\left(y_{i} | \mathbf{x}{i}^{\mathrm{RP}}\right) | P\left(y{i} | \mathbf{x}_{i}\right) \right) $$
The gradients obtained for the modified log-likelihood is as follows:
$$ \eta \Delta_{L P}\left(x_{t}\right)= \alpha \cdot \left[ I\left(y_{t}=1\right)-P\left(y_{t}=1 ; \psi\right) \right] + (1- \alpha) \cdot\left[\beta_{t} \cdot n_{t}\left(x_{t}\right)-\beta_{f} \cdot n_{f}\left(x_{t}\right)\right] $$
$$ \Delta_{R P}\left(x_{i}\right)=I\left(y_{t}=1\right) -P\left(y_{t}=1 ; \psi\right) -\alpha \cdot\left(P\left(y_{t}=1 | \mathrm{x}{l}^{\mathrm{CF}}\right)-P{D}\left(y_{t}=1 | \mathrm{x}_{t}^{\mathrm{RP}}\right)\right) $$
– Odom and Natarajan (2016) also introduced active advice seeking a framework for PLMs where model can query the human expert in the most useful areas of the feature space takes full advantage of the data as well as the expert. Advice here is a set of Queries from the model and responses from the expert. Each query is a conjunction of literals which represents set of examples and expert response is a preferred or avoid labels for that query.
Key idea here is how generate the query. Model calculates the score of each example from the entropy of prediction
$$ H\left(x_{i}\right)=\sum_{l \in \text {Labels}} P_{l}\left(y_{i} | x_{i}\right) \log \left(P_{l}\left(y_{i} | x_{i}\right)\right) $$
These scores are used as regression values and a set of weighted first-order-logic clauses are learned that group examples. These clauses are posed as query to the expert.
Conclusion
There are ways to incorporate the rich domain knowledge gathered by humans over course of time and hence we should not reinvent the wheel by making our model learn solely from the data. There can be situations where learning from data is enough but for complex and rich models it would not be sufficient and such approaches can be very useful in that case.