
harsha kokel
Learning Symbolic Representations for planning
In the pursuit of learning planner from data, I ended up reading Konidaris et al. (JAIR 2018). Getting through this paper was an onerous task. Which I would not like to do again. So, here are my notes on the key concepts from that paper, which are relevant for learning high-level, abstract planner.
This paper learns abstract symbolic representations from lower level trajectories for planning at a high-level. Big Idea of this paper is that given different domains of increasing difficulty at lower level but similar high level tasks, if we are able to segregate the low-level and high-level tasks, the tasks can be considered equivalent at higher level and hence can be solved in a uniform manner.
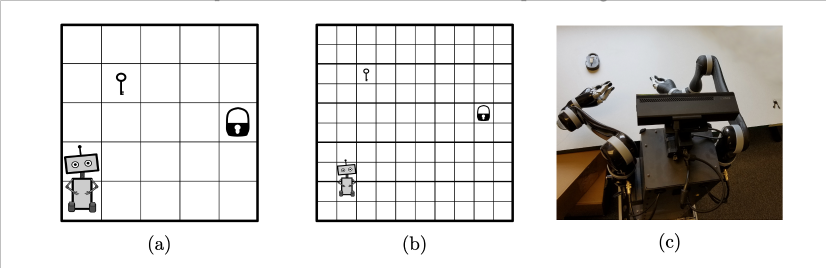
For example, given three tasks as shown above:
- A 5 x 5 grid world were agent has to take the key and open the lock or
- Same task for 10 x 10 grid or
- Robot running around the room trying to unlock a cupboard in continuous state and action space.
If we are given low level skills in each of the domain like navigating to a location and picking up the key or opening a lock, then high level plan in all these domains is equivalent. So, how to learn the abstractions which can help us plan at higher level? And ensure that the plan generated from such abstractions are executable with certainty?
To build a high level abstract planner, they use the options framework at the low-level. Operators in planning is equivalent to the options, precondition of an operator can be seen as initiation set and the effects of the operator can be seen as termination condition.

Since operators in planning only impact subset of variables and leave others unchange, this can be seen as factored MDP.
A plan is feasible if it can be executed and it is satisfiable if it is feasible and reaches goal state. To ensure plan is feasible and satisfiable, we need to learn precondition, effect and remainder for each abstract operator. Precondition indicates the necessary conditions for taking action, effect indicates the changes in the state because of taking action, and remainder indicates variables which are unaffected by the action.
I appreciate the details authors provide to prove the above intuition. May be I will add the proof here later.
To infer these three things, authors prove that learning following classifier for each abstract action is sufficient:
- $precondition(X,o)$ – a classifier that indicates if option $o$ can be performed in the state $X$. This is equivalent to initiation set $I_o$.
- $effects(X,o)$ – a classifier that indicates if state $X$ belongs to effect set of the option $o$
- $mask(o)$ – a set of variables that are modified by option $o$
From the above three functions, we can infer the remainder and image set of option $o$ as follows:
Image $Im(X,o)$ – set of state obtained after executing option $o$ in state set $X$
$Remainder(X,o)$ – possible states with same values as $X$ for all variables except $mask(o)$
$$ Remainder(X,o) = Project(X, mask(o))$$ $$Im(X,o) = Effects(X,o) \cap Remainder(X,o)$$
Thus we can learn PDDL operators directly from the trajectories and leverage the rich planning literature to perform high level planning in RL tasks.
References
George Konidaris, Leslie Pack Kaelbling, Tomas Lozano-Perez, From Skills to Symbols: Learning Symbolic Representations for Abstract High-Level Planning, JAIR 2018